ค.ร.น. ของ 10 และ 14 คือ 70
ห.ร.ม. ของ 10 และ 14 คือ 2
| ผลคูณของจำนวนนับสองจำนวน | = ผลคูณของ ค.ร.น. และ ห.ร.ม. ของจำนวนนับสองจำนวนนั้น |
| 10 x 14 | = 70 x 2 |
| 140 | = 140 |
ความแตกต่างระหว่าง ค.ร.น. และ ห.ร.ม.
 | ค.ร.น. ของ 10 และ 14 คือ ตัวตั้งที่มีค่าน้อยที่สุดที่ หารด้วย 10 และ 14 ลงตัว ห.ร.ม. ของ 10 และ 14 คือ ตัวหารที่มีค่ามากที่สุดที่นำไปหาร 10 และ 14 ลงตัว |
การวิเคราะห์โจทย์ปัญหา ค.ร.น. และ ห.ร.ม.
นักเรียนหลายคนทำโจทย์ ค.ร.น. และ ห.ร.ม. โดยไม่ได้วิเคราะห์โจทย์ แต่สังเกตคำว่า "น้อยที่สุด" หรือ "มากที่สุด" ในโจทย์
ถ้าพบคำว่า "น้อยที่สุด" ในโจทย์ข้อใด จะทำโจทย์ข้อนั้นด้วย ค.ร.น. เพราะคิดแค่ "น้อยที่สุด" คือ คูณร่วมน้อย (ค.ร.น.)
ถ้าพบคำว่า "มากที่สุด" ในโจทย์ข้อใด จะทำโจทย์ข้อนั้นด้วย ห.ร.ม. เพราะคิดแค่ "มากที่สุด" คือ หารร่วมมาก (ห.ร.ม.)
วิธีคิดแบบนี้มีโอกาสที่จะทำโจทย์ผิดเพราะ "น้อยที่สุด" ในโจทย์บางข้อต้องคำนวณคำตอบด้วย ห.ร.ม. และ "มากที่สุด" ในโจทย์บางข้อต้องคำนวณคำตอบด้วย ค.ร.น. การเลือกใช้ ค.ร.น หรือ ห.ร.ม. ในโจทย์แต่ละข้อ ต้องวิเคราะห์จากเนื้อหาของโจทย์เป็นหลัก ไม่ใช่ยึดติดกับคำว่า "น้อยที่สุด" หรือ "มากที่สุด"
| ตัวอย่างต่อไปนี้ | แสดงให้เห็นว่าโจทย์เลข ค.ร.น. สามารถอยู่คู่กับคำว่า "น้อยที่สุด" หรือ "มากที่สุด" ก็ได้ |
| ขณะเดียวกันโจทย์เลข ห.ร.ม. ก็สามารถอยู่คู่กับคำว่า "มากที่สุด" หรือ "น้อยที่สุด" ก็ได้ |

| โรงเรียนพาเนตรนารี และ ลูกเสือไปร่วมโครงการเข้าค่ายปลูกป่า ผู้จัดโครงการได้เตรียมที่ดินสำหรับโครงการนี้ไว้ 2 แปลง แปลงละ 10 ไร่ เนตรนารี 24 คน ตั้งค่ายในที่ดินแปลงที่อยู่ทางฝั่งตะวันตกของลำธาร ลูกเสือ 30 คน ตั้งค่ายในที่ดินแปลงที่อยู่ทางฝั่งตะวันออกของลำธาร เนตรนารีและลูกเสือปลูกต้นไม้ทางทิศเหนือของที่ดิน และสร้างกระท่อมสำหรับพักทางทิศใต้ กระท่อมแต่ละหลังรองรับจำนวนคนเท่ากัน กระท่อมทุกหลังต้องจัดให้มีคนพักเต็ม เนตรนารีและลูกเสือไม่พักในกระท่อมหลังเดียวกัน เนตรนารีและลูกเสือทุกคนต้องได้พักในกระท่อม ต้องการให้กระท่อมแต่ละหลังรองรับจำนวนคนได้มากที่สุด กระท่อมแต่ละหลังรองรับคนได้กี่คน ? สมมุติให้กระท่อมแต่ละหลังรองรับคนได้ A คน
A คือจำนวนที่มีค่ามากที่สุดที่หาร 24 และ 30 ลงตัว ดังนั้น A คือ ห.ร.ม. ของ 24 และ 30 หา ห.ร.ม. ของ 24 และ 30 ได้ 3 วิธี
|
หา ห.ร.ม. ด้วยวิธีตั้งหารแบบยูคลิด
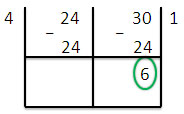
ห.ร.ม. ของ 24 และ 30 คือ 6
ต้องการให้กระท่อมแต่ละหลังรองรับจำนวนคนได้มากที่สุด กระท่อมแต่ละหลังรองรับคนได้ 6 คน
ข้อสังเกต โจทย์คำถามมีคำว่า มากที่สุด คำนวณคำตอบโดยใช้ หารร่วมมาก (ห.ร.ม.)
ต้องการสร้างกระท่อมน้อยที่สุด ต้องสร้างกระท่อมกี่หลัง ?
"จำนวนกระท่อม" และ "จำนวนคนในกระท่อมแต่ละหลัง" มีความสัมพันธ์ในทิศตรงข้ามกัน
| เนื่องจากจำนวนเนตรนารีและลูกเสือคงที่ | ถ้า ลด "จำนวนคนในกระท่อมแต่ละหลัง" จะทำให้ "จำนวนกระท่อม" เพิ่มขึ้น |
| ถ้า เพิ่ม "จำนวนคนในกระท่อมแต่ละหลัง" จะทำให้ "จำนวนกระท่อม" ลดลง |
หาจำนวนคนที่กระท่อมแต่ละหลังสามารถรองรับคนได้มากที่สุดโดยคำนวณด้วย ห.ร.ม.
กระท่อมแต่ละหลังรองรับคนได้มากที่สุด 6 คน
เนตรนารี 24 คน พักในกระท่อมหลังละ 6 คน ต้องสร้างกระท่อมให้เนตรนารีกี่หลัง ?
ลูกเสือ 30 คน พักในกระท่อมหลังละ 6 คน ต้องสร้างกระท่อมให้ลูกเสือกี่หลัง ?
ต้องการสร้างกระท่อมน้อยที่สุด ต้องสร้างกระท่อม 9 หลัง
จำนวนต้นไม้ที่ปลูกทางทิศเหนือของที่ดินทั้งสองแปลงเท่ากัน ลูกเสือแต่ละคนปลูกต้นไม้เท่ากัน เนตรนารีแต่ละคนปลูกต้นไม้เท่ากัน ต้องการปลูกต้นไม้น้อยที่สุด ที่ดินแต่ละแปลงปลูกต้นไม้กี่ต้น สมมุติว่าที่ดินแต่ละแปลงปลูกต้นไม้ B ต้น
B คือจำนวนที่มีค่าน้อยที่สุดที่หารด้วย 24 และ 30 ลงตัว ดังนั้น B คือ ค.ร.น. ของ 24 และ 30 |
| หา ค.ร.น.ด้วยวิธีแยกตัวประกอบ 24 = 2 x 3 x 2 x 2 30 = 2 x 3 x 5
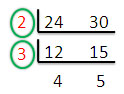
| หา ค.ร.น. ด้วยวิธีหารด้วยตัวประกอบร่วม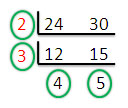
|
ต้องการปลูกต้นไม้น้อยที่สุด ที่ดินแต่ละแปลงปลูกต้นไม้ 120 ต้น
ข้อสังเกต โจทย์คำถามมีคำว่า น้อยที่สุด คำนวณคำตอบโดยใช้ คูณร่วมน้อย (ค.ร.น.)
ต้นไม้แต่ละต้นปลูกให้มีระยะห่างเท่ากัน
เพื่อให้มีที่ดินสำหรับสร้างกระท่อมมากที่สุด ลูกเสือและเนตรนารีต้องปลูกต้นไม้คนละกี่ต้น ?
"ขนาดของพื้นที่ปลูกต้นไม้" และ "ขนาดของพื้นที่สร้างกระท่อม" มีความสัมพันธ์ในทิศทางตรงข้ามกัน
| เนื่องจากขนาดของที่ดินแต่ละแปลงคงที่ | ถ้า เพิ่ม "ขนาดของพื้นที่ปลูกต้นไม้" จะทำให้ "ขนาดของพื้นที่สร้างกระท่อม" ลดลง |
| ถ้า ลด "ขนาดของพื้นที่ปลูกต้นไม้" จะทำให้ "ขนาดของพื้นที่สร้างกระท่อม" เพิ่มขึ้น |
คำนวณจำนวนต้นไม้ที่น้อยที่สุดที่ปลูกในที่ดินแต่ละแปลง โดยใช้ ค.ร.น.
ต้องการปลูกต้นไม้น้อยที่สุด ที่ดินแต่ละแปลงปลูกต้นไม้ 120 ต้น
เนตรนารี 24 คน ปลูกต้นไม้ 120 ต้น เนตรนารีแต่ละคนปลูกต้นไม้กี่ต้น ?
| เนตรนารีแต่ละคนปลูกต้นไม้ | = 120 ÷ 24 |
| = 5 ต้น |
ลูกเสือ 30 คน ปลูกต้นไม้ 120 ต้น ลูกเสือแต่ละคนปลูกต้นไม้กี่ต้น ?
| ลูกเสือแต่ละคนปลูกต้นไม้ | = 120 ÷ 30 |
| = 4 ต้น |
เพื่อให้มีที่ดินสำหรับสร้างกระท่อมมากที่สุด เนตรนารีปลูกต้นไม้คนละ 5 ต้น ลูกเสือต้องปลูกต้นไม้คนละ 4 ต้น
ข้อสังเกต โจทย์คำถามมีคำว่า มากที่สุด คำนวณคำตอบโดยใช้ คูณร่วมน้อย (ค.ร.น.)
ตัวอย่างที่ผ่านมาแสดงให้เห็นว่า การทำโจทย์ ค.ร.น. และ ห.ร.ม. ให้ได้คำตอบถูกต้องทุกครั้ง ต้องอาศัยการวิเคราะห์เนื้อหาของโจทย์ นักเรียนต้องสามารถวิเคราะห์ได้ว่าเหตุการณ์ต่าง ๆ ในโจทย์มีความสัมพันธ์กันอย่างไร ส่งผลต่อคำตอบอย่างไร จึงจะเลือกใช้ ค.ร.น. หรือ ห.ร.ม. ได้อย่างถูกต้อง
นักเรียนที่ไม่สามารถวิเคราะห์โจทย์ได้ ต้องฝึก พัฒนาทักษะการวิเคราะห์โดยฝึกวิเคราะห์โจทย์ที่มีเนื้อหาหลากหลาย
โจทย์สำหรับให้นักเรียนฝึกวิเคราะห์ถูกจัดเตรียมไว้ที่ท้ายบทความนี้ ให้คลิกที่ลิงค์ แบบฝึกหัด "ค.ร.น. และ ห.ร.ม. "
ไม่มีความคิดเห็น:
แสดงความคิดเห็น